Lab 06: Code introspection and metaprogramming
In this lab we are first going to inspect some tooling to help you understand what Julia does under the hood such as:
looking at the code at different levels
understanding what method is being called
showing different levels of code optimization
Secondly we will start playing with the metaprogramming side of Julia, mainly covering:
how to view abstract syntax tree (AST) of Julia code
how to manipulate AST
These topics will be extended in the next lecture/lab, where we are going use metaprogramming to manipulate code with macros.
We will be again a little getting ahead of ourselves as we are going to use quite a few macros, which will be properly explained in the next lecture as well, however for now the important thing to know is that a macro is just a special function, that accepts as an argument Julia code, which it can modify.
Quick reminder of introspection tooling
Let's start with the topic of code inspection, e.g. we may ask the following: What happens when Julia evaluates [i for i in 1:10]?
parsing
julia> :([i for i in 1:10]) |> dump
Expr
head: Symbol comprehension
args: Array{Any}((1,))
1: Expr
head: Symbol generator
args: Array{Any}((2,))
1: Symbol i
2: Expr
head: Symbol =
args: Array{Any}((2,))
1: Symbol i
2: Expr
head: Symbol call
args: Array{Any}((3,))
1: Symbol :
2: Int64 1
3: Int64 10lowering
julia> Meta.@lower debuginfo=:none [i for i in 1:10]ERROR: MethodError: no method matching lower(::Symbol, ::Expr)
The function `lower` exists, but no method is defined for this combination of argument types.
Closest candidates are:
lower(::Module, ::Any)
@ Base meta.jl:163typing
julia> f() = [i for i in 1:10]f (generic function with 1 method)julia> @code_typed debuginfo=:none f()CodeInfo(
1 ── %1 = builtin Core.memorynew(Memory{Int64}, 10)::Memory{Int64}
│ %2 = builtin Core.memoryrefnew(%1)::MemoryRef{Int64}
│ %3 = %new(Vector{Int64}, %2, (10,))::Vector{Int64}
│ %4 = $(Expr(:boundscheck, true))::Bool
└─── goto #5 if not %4
2 ── %6 = intrinsic Base.sub_int(1, 1)::Int64
│ %7 = intrinsic Base.bitcast(UInt64, %6)::UInt64
│ %8 = builtin Base.getfield(%3, :size)::Tuple{Int64}
│ %9 = $(Expr(:boundscheck, true))::Bool
│ %10 = builtin Base.getfield(%8, 1, %9)::Int64
│ %11 = intrinsic Base.bitcast(UInt64, %10)::UInt64
│ %12 = intrinsic Base.ult_int(%7, %11)::Bool
└─── goto #4 if not %12
3 ── goto #5
4 ── %15 = builtin Core.tuple(1)::Tuple{Int64}
│ invoke Base.throw_boundserror(%3::Vector{Int64}, %15::Tuple{Int64})::Union{}
└─── unreachable
5 ┄─ %18 = builtin Base.getfield(%3, :ref)::MemoryRef{Int64}
│ %19 = builtin Base.memoryrefnew(%18, 1, false)::MemoryRef{Int64}
│ builtin Base.memoryrefset!(%19, 1, :not_atomic, false)::Int64
└─── goto #6
6 ── goto #7
7 ── nothing::Nothing
8 ┄─ %24 = φ (#7 => 2, #22 => %59)::Int64
│ %25 = φ (#7 => 1, #22 => %33)::Int64
│ %26 = builtin (%25 === 10)::Bool
└─── goto #10 if not %26
9 ── goto #11
10 ─ %29 = intrinsic Base.add_int(%25, 1)::Int64
└─── goto #11
11 ┄ %31 = φ (#9 => true, #10 => false)::Bool
│ %32 = φ (#10 => %29)::Int64
│ %33 = φ (#10 => %29)::Int64
└─── goto #13 if not %31
12 ─ goto #14
13 ─ goto #14
14 ┄ %37 = φ (#12 => true, #13 => false)::Bool
└─── goto #16 if not %37
15 ─ goto #23
16 ─ %40 = $(Expr(:boundscheck, false))::Bool
└─── goto #20 if not %40
17 ─ %42 = intrinsic Base.sub_int(%24, 1)::Int64
│ %43 = intrinsic Base.bitcast(UInt64, %42)::UInt64
│ %44 = builtin Base.getfield(%3, :size)::Tuple{Int64}
│ %45 = $(Expr(:boundscheck, true))::Bool
│ %46 = builtin Base.getfield(%44, 1, %45)::Int64
│ %47 = intrinsic Base.bitcast(UInt64, %46)::UInt64
│ %48 = intrinsic Base.ult_int(%43, %47)::Bool
└─── goto #19 if not %48
18 ─ goto #20
19 ─ %51 = builtin Core.tuple(%24)::Tuple{Int64}
│ invoke Base.throw_boundserror(%3::Vector{Int64}, %51::Tuple{Int64})::Union{}
└─── unreachable
20 ┄ %54 = builtin Base.getfield(%3, :ref)::MemoryRef{Int64}
│ %55 = builtin Base.memoryrefnew(%54, %24, false)::MemoryRef{Int64}
│ builtin Base.memoryrefset!(%55, %32, :not_atomic, false)::Int64
└─── goto #21
21 ─ goto #22
22 ─ %59 = intrinsic Base.add_int(%24, 1)::Int64
└─── goto #8
23 ─ goto #24
24 ─ goto #25
25 ─ goto #26
26 ─ return %3
) => Vector{Int64}LLVM code generation
julia> @code_llvm debuginfo=:none f(); Function Signature: f()
define nonnull ptr @julia_f_26185() #0 {
L18:
%gcframe1 = alloca [3 x ptr], align 16
call void @llvm.memset.p0.i64(ptr align 16 %gcframe1, i8 0, i64 24, i1 true)
%thread_ptr = call ptr asm "movq %fs:0, $0", "=r"() #10
%tls_ppgcstack = getelementptr inbounds i8, ptr %thread_ptr, i64 -8
%tls_pgcstack = load ptr, ptr %tls_ppgcstack, align 8
store i64 4, ptr %gcframe1, align 8
%frame.prev = getelementptr inbounds ptr, ptr %gcframe1, i64 1
%task.gcstack = load ptr, ptr %tls_pgcstack, align 8
store ptr %task.gcstack, ptr %frame.prev, align 8
store ptr %gcframe1, ptr %tls_pgcstack, align 8
%ptls_field = getelementptr inbounds i8, ptr %tls_pgcstack, i64 16
%ptls_load = load ptr, ptr %ptls_field, align 8
%"Memory{Int64}[]" = call noalias nonnull align 8 dereferenceable(112) ptr @ijl_gc_small_alloc(ptr %ptls_load, i32 648, i32 112, i64 139949111749392) #6
%"Memory{Int64}[].tag_addr" = getelementptr inbounds i64, ptr %"Memory{Int64}[]", i64 -1
store atomic i64 139949111749392, ptr %"Memory{Int64}[].tag_addr" unordered, align 8
%memory_ptr = getelementptr inbounds { i64, ptr }, ptr %"Memory{Int64}[]", i64 0, i32 1
%memory_data = getelementptr inbounds i8, ptr %"Memory{Int64}[]", i64 16
store ptr %memory_data, ptr %memory_ptr, align 8
store i64 10, ptr %"Memory{Int64}[]", align 8
%gc_slot_addr_0 = getelementptr inbounds ptr, ptr %gcframe1, i64 2
store ptr %"Memory{Int64}[]", ptr %gc_slot_addr_0, align 8
%ptls_load33 = load ptr, ptr %ptls_field, align 8
%"new::Array" = call noalias nonnull align 8 dereferenceable(32) ptr @ijl_gc_small_alloc(ptr %ptls_load33, i32 408, i32 32, i64 139949054530672) #6
%"new::Array.tag_addr" = getelementptr inbounds i64, ptr %"new::Array", i64 -1
store atomic i64 139949054530672, ptr %"new::Array.tag_addr" unordered, align 8
%0 = getelementptr inbounds i8, ptr %"new::Array", i64 8
store ptr %memory_data, ptr %"new::Array", align 8
store ptr %"Memory{Int64}[]", ptr %0, align 8
%"new::Array.size_ptr" = getelementptr inbounds i8, ptr %"new::Array", i64 16
store i64 10, ptr %"new::Array.size_ptr", align 8
store <4 x i64> <i64 1, i64 2, i64 3, i64 4>, ptr %memory_data, align 8
%gep.3 = getelementptr inbounds i8, ptr %"Memory{Int64}[]", i64 48
store <4 x i64> <i64 5, i64 6, i64 7, i64 8>, ptr %gep.3, align 8
%gep.7 = getelementptr inbounds i8, ptr %"Memory{Int64}[]", i64 80
store i64 9, ptr %gep.7, align 8
%gep.8 = getelementptr inbounds i8, ptr %"Memory{Int64}[]", i64 88
store i64 10, ptr %gep.8, align 8
%frame.prev34 = load ptr, ptr %frame.prev, align 8
store ptr %frame.prev34, ptr %tls_pgcstack, align 8
ret ptr %"new::Array"
}native code generation
julia> @code_native debuginfo=:none f() .text
.file "f"
.section .rodata.cst32,"aM",@progbits,32
.p2align 5, 0x0 # -- Begin function julia_f_26297
.LCPI0_0:
.quad 1 # 0x1
.quad 2 # 0x2
.quad 3 # 0x3
.quad 4 # 0x4
.LCPI0_1:
.quad 5 # 0x5
.quad 6 # 0x6
.quad 7 # 0x7
.quad 8 # 0x8
.section .ltext,"axl",@progbits
.globl julia_f_26297
.p2align 4, 0x90
.type julia_f_26297,@function
julia_f_26297: # @julia_f_26297
; Function Signature: f()
# %bb.0: # %L18
push rbp
mov rbp, rsp
push r15
push r14
push r13
push r12
push rbx
sub rsp, 24
vxorps xmm0, xmm0, xmm0
vmovaps xmmword ptr [rbp - 64], xmm0
mov qword ptr [rbp - 48], 0
#APP
mov rax, qword ptr fs:[0]
#NO_APP
lea rcx, [rbp - 64]
movabs rbx, 139949054530672
movabs r13, offset ijl_gc_small_alloc
mov esi, 648
mov edx, 112
mov r12, qword ptr [rax - 8]
mov qword ptr [rbp - 64], 4
lea r14, [rbx + 57218720]
mov rax, qword ptr [r12]
mov qword ptr [rbp - 56], rax
mov qword ptr [r12], rcx
mov rcx, r14
mov rdi, qword ptr [r12 + 16]
call r13
mov qword ptr [rax - 8], r14
lea r14, [rax + 16]
mov qword ptr [rbp - 48], rax
mov esi, 408
mov edx, 32
mov r15, rax
mov rcx, rbx
mov qword ptr [rax + 8], r14
mov qword ptr [rax], 10
mov rdi, qword ptr [r12 + 16]
call r13
movabs rcx, offset .LCPI0_0
mov qword ptr [rax - 8], rbx
mov qword ptr [rax], r14
mov qword ptr [rax + 8], r15
mov qword ptr [rax + 16], 10
vmovaps ymm0, ymmword ptr [rcx]
movabs rcx, offset .LCPI0_1
vmovaps ymm1, ymmword ptr [rcx]
mov rcx, qword ptr [rbp - 56]
vmovups ymmword ptr [r15 + 16], ymm0
vmovups ymmword ptr [r15 + 48], ymm1
mov qword ptr [r15 + 80], 9
mov qword ptr [r15 + 88], 10
mov qword ptr [r12], rcx
add rsp, 24
pop rbx
pop r12
pop r13
pop r14
pop r15
pop rbp
vzeroupper
ret
.Lfunc_end0:
.size julia_f_26297, .Lfunc_end0-julia_f_26297
# -- End function
.type ".L_j_const#2",@object # @"_j_const#2"
.section .rodata.cst8,"aM",@progbits,8
.p2align 3, 0x0
".L_j_const#2":
.quad 1 # 0x1
.size ".L_j_const#2", 8
.set ".L+Core.Array#26300.jit", 139949054530672
.size ".L+Core.Array#26300.jit", 8
.set ".L+Core.GenericMemory#26299.jit", 139949111749392
.size ".L+Core.GenericMemory#26299.jit", 8
.section ".note.GNU-stack","",@progbitsLet's see how these tools can help us understand some of Julia's internals on examples from previous labs and lectures.
Understanding runtime dispatch and type instabilities
We will start with a question: Can we spot internally some difference between type stable/unstable code?
Exercise
Inspect the following two functions using @code_lowered, @code_typed, @code_llvm and @code_native.
x = rand(10^5)
function explicit_len(x)
length(x)
end
function implicit_len()
length(x)
endFor now do not try to understand the details, but focus on the overall differences such as length of the code.
Redirecting stdout
If the output of the method introspection tools is too long you can use a general way of redirecting standard output stdout to a file
open("./llvm_fun.ll", "w") do file
original_stdout = stdout
redirect_stdout(file)
@code_llvm debuginfo=:none fun()
redirect_stdout(original_stdout)
endIn case of @code_llvm and @code_native there are special options, that allow this out of the box, see help ? for underlying code_llvm and code_native. If you don't mind adding dependencies there is also the @capture_out from Suppressor.jl
:::
Details
@code_warntype explicit_len(x)
@code_warntype implicit_len()
@code_typed debuginfo=:none explicit_len(x)
@code_typed debuginfo=:none implicit_len()
@code_llvm debuginfo=:none explicit_len(x)
@code_llvm debuginfo=:none implicit_len()
@code_native debuginfo=:none explicit_len(x)
@code_native debuginfo=:none implicit_len()In this case we see that the generated code for such a simple operation is much longer in the type unstable case resulting in longer run times. However in the next example we will see that having longer code is not always a bad thing.
Loop unrolling
In some cases the compiler uses loop unrolling[1] optimization to speed up loops at the expense of binary size. The result of such optimization is removal of the loop control instructions and rewriting the loop into a repeated sequence of independent statements.
Exercise
Inspect under what conditions does the compiler unroll the for loop in the polynomial function from the last lab.
function polynomial(a, x)
accumulator = a[end] * one(x)
for i in length(a)-1:-1:1
accumulator = accumulator * x + a[i]
end
accumulator
endCompare the speed of execution with and without loop unrolling.
HINTS:
these kind of optimization are lower level than intermediate language
loop unrolling is possible when compiler knows the length of the input
Details
using BenchmarkTools
a = Tuple(ones(20)) # tuple has known size
ac = collect(a)
x = 2.0
@code_lowered polynomial(a,x) # cannot be seen here as optimizations are not applied
@code_typed debuginfo=:none polynomial(a,x) # loop unrolling is not part of type inference optimizationMore than 2x speedup
julia> @btime polynomial($a,$x)
9.025 ns (0 allocations: 0 bytes)
1.048575e6
julia> @btime polynomial($ac,$x)
19.443 ns (0 allocations: 0 bytes)
1.048575e6julia> @code_llvm debuginfo=:none polynomial(a,x); Function Signature: polynomial(NTuple{20, Float64}, Float64)
define double @julia_polynomial_27306(ptr nocapture noundef nonnull readonly align 8 dereferenceable(160) %"a::Tuple", double %"x::Float64") #0 {
pass.18:
%"a::Tuple[20]_ptr" = getelementptr inbounds i8, ptr %"a::Tuple", i64 152
%"a::Tuple[20]_ptr.unbox" = load double, ptr %"a::Tuple[20]_ptr", align 8
%0 = fmul double %"a::Tuple[20]_ptr.unbox", %"x::Float64"
%1 = getelementptr inbounds double, ptr %"a::Tuple", i64 18
%.unbox = load double, ptr %1, align 8
%2 = fadd double %0, %.unbox
%3 = fmul double %2, %"x::Float64"
%4 = getelementptr inbounds double, ptr %"a::Tuple", i64 17
%.unbox.1 = load double, ptr %4, align 8
%5 = fadd double %3, %.unbox.1
%6 = fmul double %5, %"x::Float64"
%7 = getelementptr inbounds double, ptr %"a::Tuple", i64 16
%.unbox.2 = load double, ptr %7, align 8
%8 = fadd double %6, %.unbox.2
%9 = fmul double %8, %"x::Float64"
%10 = getelementptr inbounds double, ptr %"a::Tuple", i64 15
%.unbox.3 = load double, ptr %10, align 8
%11 = fadd double %9, %.unbox.3
%12 = fmul double %11, %"x::Float64"
%13 = getelementptr inbounds double, ptr %"a::Tuple", i64 14
%.unbox.4 = load double, ptr %13, align 8
%14 = fadd double %12, %.unbox.4
%15 = fmul double %14, %"x::Float64"
%16 = getelementptr inbounds double, ptr %"a::Tuple", i64 13
%.unbox.5 = load double, ptr %16, align 8
%17 = fadd double %15, %.unbox.5
%18 = fmul double %17, %"x::Float64"
%19 = getelementptr inbounds double, ptr %"a::Tuple", i64 12
%.unbox.6 = load double, ptr %19, align 8
%20 = fadd double %18, %.unbox.6
%21 = fmul double %20, %"x::Float64"
%22 = getelementptr inbounds double, ptr %"a::Tuple", i64 11
%.unbox.7 = load double, ptr %22, align 8
%23 = fadd double %21, %.unbox.7
%24 = fmul double %23, %"x::Float64"
%25 = getelementptr inbounds double, ptr %"a::Tuple", i64 10
%.unbox.8 = load double, ptr %25, align 8
%26 = fadd double %24, %.unbox.8
%27 = fmul double %26, %"x::Float64"
%28 = getelementptr inbounds double, ptr %"a::Tuple", i64 9
%.unbox.9 = load double, ptr %28, align 8
%29 = fadd double %27, %.unbox.9
%30 = fmul double %29, %"x::Float64"
%31 = getelementptr inbounds double, ptr %"a::Tuple", i64 8
%.unbox.10 = load double, ptr %31, align 8
%32 = fadd double %30, %.unbox.10
%33 = fmul double %32, %"x::Float64"
%34 = getelementptr inbounds double, ptr %"a::Tuple", i64 7
%.unbox.11 = load double, ptr %34, align 8
%35 = fadd double %33, %.unbox.11
%36 = fmul double %35, %"x::Float64"
%37 = getelementptr inbounds double, ptr %"a::Tuple", i64 6
%.unbox.12 = load double, ptr %37, align 8
%38 = fadd double %36, %.unbox.12
%39 = fmul double %38, %"x::Float64"
%40 = getelementptr inbounds double, ptr %"a::Tuple", i64 5
%.unbox.13 = load double, ptr %40, align 8
%41 = fadd double %39, %.unbox.13
%42 = fmul double %41, %"x::Float64"
%43 = getelementptr inbounds double, ptr %"a::Tuple", i64 4
%.unbox.14 = load double, ptr %43, align 8
%44 = fadd double %42, %.unbox.14
%45 = fmul double %44, %"x::Float64"
%46 = getelementptr inbounds double, ptr %"a::Tuple", i64 3
%.unbox.15 = load double, ptr %46, align 8
%47 = fadd double %45, %.unbox.15
%48 = fmul double %47, %"x::Float64"
%49 = getelementptr inbounds double, ptr %"a::Tuple", i64 2
%.unbox.16 = load double, ptr %49, align 8
%50 = fadd double %48, %.unbox.16
%51 = fmul double %50, %"x::Float64"
%52 = getelementptr inbounds double, ptr %"a::Tuple", i64 1
%.unbox.17 = load double, ptr %52, align 8
%53 = fadd double %51, %.unbox.17
%54 = fmul double %53, %"x::Float64"
%.unbox.18 = load double, ptr %"a::Tuple", align 8
%55 = fadd double %54, %.unbox.18
ret double %55
}julia> @code_llvm debuginfo=:none polynomial(ac,x); Function Signature: polynomial(Array{Float64, 1}, Float64)
define double @julia_polynomial_27310(ptr noundef nonnull align 8 dereferenceable(24) %"a::Array", double %"x::Float64") #0 {
top:
%"new::Tuple" = alloca [1 x i64], align 8
%"new::Tuple34" = alloca [1 x i64], align 8
%"a::Array.size_ptr" = getelementptr inbounds i8, ptr %"a::Array", i64 16
%"a::Array.size.0.copyload" = load i64, ptr %"a::Array.size_ptr", align 8
%0 = add i64 %"a::Array.size.0.copyload", -1
%.not.not = icmp eq i64 %"a::Array.size.0.copyload", 0
br i1 %.not.not, label %L15, label %L18
L15: ; preds = %top
store i64 0, ptr %"new::Tuple34", align 8
call void @j_throw_boundserror_27313(ptr nonnull %"a::Array", ptr nocapture nonnull readonly %"new::Tuple34") #12
unreachable
L18: ; preds = %top
%memoryref_data = load ptr, ptr %"a::Array", align 8
%memoryref_offset = shl i64 %"a::Array.size.0.copyload", 3
%1 = getelementptr i8, ptr %memoryref_data, i64 %memoryref_offset
%memoryref_data4 = getelementptr i8, ptr %1, i64 -8
%2 = load double, ptr %memoryref_data4, align 8
%3 = icmp sgt i64 %0, 0
br i1 %3, label %L78.preheader, label %L64
L64: ; preds = %L18
%.not40.not.not.not = icmp eq i64 %"a::Array.size.0.copyload", -9223372036854775808
br i1 %.not40.not.not.not, label %L78.preheader, label %L112
L78.preheader: ; preds = %L64, %L18
%value_phi47 = phi i64 [ -9223372036854775808, %L64 ], [ 1, %L18 ]
%invariant.gep = getelementptr i8, ptr %memoryref_data, i64 -8
br label %L78
L78: ; preds = %L96, %L78.preheader
%value_phi10 = phi i64 [ %4, %L96 ], [ %0, %L78.preheader ]
%value_phi12 = phi double [ %7, %L96 ], [ %2, %L78.preheader ]
%4 = add i64 %value_phi10, -1
%.not41 = icmp ult i64 %4, %"a::Array.size.0.copyload"
br i1 %.not41, label %L96, label %L93
L93: ; preds = %L78
store i64 %value_phi10, ptr %"new::Tuple", align 8
call void @j_throw_boundserror_27313(ptr nonnull %"a::Array", ptr nocapture nonnull readonly %"new::Tuple") #12
unreachable
L96: ; preds = %L78
%5 = fmul double %value_phi12, %"x::Float64"
%memoryref_offset19 = shl i64 %value_phi10, 3
%gep = getelementptr i8, ptr %invariant.gep, i64 %memoryref_offset19
%6 = load double, ptr %gep, align 8
%7 = fadd double %5, %6
%.not42.not = icmp eq i64 %value_phi10, %value_phi47
br i1 %.not42.not, label %L112, label %L78
L112: ; preds = %L96, %L64
%value_phi29 = phi double [ %2, %L64 ], [ %7, %L96 ]
ret double %value_phi29
}Recursion inlining depth
Inlining[2] is another compiler optimization that allows us to speed up the code by avoiding function calls. Where applicable compiler can replace f(args) directly with the function body of f, thus removing the need to modify stack to transfer the control flow to a different place. This is yet another optimization that may improve speed at the expense of binary size.
Exercise
Rewrite the polynomial function from the last lab using recursion and find the length of the coefficients, at which inlining of the recursive calls stops occurring.
function polynomial(a, x)
accumulator = a[end] * one(x)
for i in length(a)-1:-1:1
accumulator = accumulator * x + a[i]
end
accumulator
endHINTS:
define two methods
_polynomial!(ac, x, a...)and_polynomial!(ac, x, a)for the case of ≥2 coefficients and the last coefficientuse splatting together with range indexing
a[1:end-1]...the correctness can be checked using the built-in
evalpolyrecall that these kind of optimization are possible just around the type inference stage
use container of known length to store the coefficients
Splatting/slurping operator ...
The operator ... serves two purposes inside function calls [3][4]:
- combines multiple arguments into one
julia> function printargs(args...)
println(typeof(args))
for (i, arg) in enumerate(args)
println("Arg #$i = $arg")
end
end
printargs (generic function with 1 method)
julia> printargs(1, 2, 3)
Tuple{Int64, Int64, Int64}
Arg #1 = 1
Arg #2 = 2
Arg #3 = 3- splits one argument into many different arguments
julia> function threeargs(a, b, c)
println("a = $a::$(typeof(a))")
println("b = $b::$(typeof(b))")
println("c = $c::$(typeof(c))")
end
threeargs (generic function with 1 method)
julia> threeargs([1,2,3]...) # or with a variable threeargs(x...)
a = 1::Int64
b = 2::Int64
c = 3::Int64:::
Details
_polynomial!(ac, x, a...) = _polynomial!(x * ac + a[end], x, a[1:end-1]...)
_polynomial!(ac, x, a) = x * ac + a
polynomial(a, x) = _polynomial!(a[end] * one(x), x, a[1:end-1]...)
# the coefficients have to be a tuple
a = Tuple(ones(Int, 21)) # everything less than 22 gets inlined
x = 2
polynomial(a,x) == evalpoly(x,a) # compare with built-in function
# @code_llvm debuginfo=:none polynomial(a,x) # seen here too, but code_typed is a better option
@code_lowered polynomial(a,x) # cannot be seen here as optimizations are not appliedjulia> @code_typed debuginfo=:none polynomial(a,x)CodeInfo(
1 ─ %1 = $(Expr(:boundscheck, true))::Bool
│ %2 = builtin Base.getfield(a, 21, %1)::Int64
│ %3 = intrinsic Base.mul_int(%2, 1)::Int64
│ %4 = builtin Core.getfield(a, 1)::Int64
│ %5 = builtin Core.getfield(a, 2)::Int64
│ %6 = builtin Core.getfield(a, 3)::Int64
│ %7 = builtin Core.getfield(a, 4)::Int64
│ %8 = builtin Core.getfield(a, 5)::Int64
│ %9 = builtin Core.getfield(a, 6)::Int64
│ %10 = builtin Core.getfield(a, 7)::Int64
│ %11 = builtin Core.getfield(a, 8)::Int64
│ %12 = builtin Core.getfield(a, 9)::Int64
│ %13 = builtin Core.getfield(a, 10)::Int64
│ %14 = builtin Core.getfield(a, 11)::Int64
│ %15 = builtin Core.getfield(a, 12)::Int64
│ %16 = builtin Core.getfield(a, 13)::Int64
│ %17 = builtin Core.getfield(a, 14)::Int64
│ %18 = builtin Core.getfield(a, 15)::Int64
│ %19 = builtin Core.getfield(a, 16)::Int64
│ %20 = builtin Core.getfield(a, 17)::Int64
│ %21 = builtin Core.getfield(a, 18)::Int64
│ %22 = builtin Core.getfield(a, 19)::Int64
│ %23 = builtin Core.getfield(a, 20)::Int64
│ %24 = intrinsic Base.mul_int(x, %3)::Int64
│ %25 = intrinsic Base.add_int(%24, %23)::Int64
│ %26 = intrinsic Base.mul_int(x, %25)::Int64
│ %27 = intrinsic Base.add_int(%26, %22)::Int64
│ %28 = intrinsic Base.mul_int(x, %27)::Int64
│ %29 = intrinsic Base.add_int(%28, %21)::Int64
│ %30 = intrinsic Base.mul_int(x, %29)::Int64
│ %31 = intrinsic Base.add_int(%30, %20)::Int64
│ %32 = intrinsic Base.mul_int(x, %31)::Int64
│ %33 = intrinsic Base.add_int(%32, %19)::Int64
│ %34 = intrinsic Base.mul_int(x, %33)::Int64
│ %35 = intrinsic Base.add_int(%34, %18)::Int64
│ %36 = intrinsic Base.mul_int(x, %35)::Int64
│ %37 = intrinsic Base.add_int(%36, %17)::Int64
│ %38 = intrinsic Base.mul_int(x, %37)::Int64
│ %39 = intrinsic Base.add_int(%38, %16)::Int64
│ %40 = intrinsic Base.mul_int(x, %39)::Int64
│ %41 = intrinsic Base.add_int(%40, %15)::Int64
│ %42 = intrinsic Base.mul_int(x, %41)::Int64
│ %43 = intrinsic Base.add_int(%42, %14)::Int64
│ %44 = intrinsic Base.mul_int(x, %43)::Int64
│ %45 = intrinsic Base.add_int(%44, %13)::Int64
│ %46 = intrinsic Base.mul_int(x, %45)::Int64
│ %47 = intrinsic Base.add_int(%46, %12)::Int64
│ %48 = intrinsic Base.mul_int(x, %47)::Int64
│ %49 = intrinsic Base.add_int(%48, %11)::Int64
│ %50 = intrinsic Base.mul_int(x, %49)::Int64
│ %51 = intrinsic Base.add_int(%50, %10)::Int64
│ %52 = intrinsic Base.mul_int(x, %51)::Int64
│ %53 = intrinsic Base.add_int(%52, %9)::Int64
│ %54 = intrinsic Base.mul_int(x, %53)::Int64
│ %55 = intrinsic Base.add_int(%54, %8)::Int64
│ %56 = intrinsic Base.mul_int(x, %55)::Int64
│ %57 = intrinsic Base.add_int(%56, %7)::Int64
│ %58 = intrinsic Base.mul_int(x, %57)::Int64
│ %59 = intrinsic Base.add_int(%58, %6)::Int64
│ %60 = intrinsic Base.mul_int(x, %59)::Int64
│ %61 = intrinsic Base.add_int(%60, %5)::Int64
│ %62 = intrinsic Base.mul_int(x, %61)::Int64
│ %63 = intrinsic Base.add_int(%62, %4)::Int64
└── return %63
) => Int64AST manipulation: The first steps to metaprogramming
Julia is so called homoiconic language, as it allows the language to reason about its code. This capability is inspired by years of development in other languages such as Lisp, Clojure or Prolog.
There are two easy ways to extract/construct the code structure [5]
- parsing code stored in string with internal
Meta.parse
julia> code_parse = Meta.parse("x = 2") # for single line expressions (additional spaces are ignored):(x = 2)julia> code_parse_block = Meta.parse("""
begin
x = 2
y = 3
x + y
end
""") # for multiline expressionsquote
#= none:2 =#
x = 2
#= none:3 =#
y = 3
#= none:4 =#
x + y
end- constructing an expression using
quote ... endor simple:()syntax
julia> code_expr = :(x = 2) # for single line expressions (additional spaces are ignored):(x = 2)julia> code_expr_block = quote
x = 2
y = 3
x + y
end # for multiline expressionsquote
#= REPL[2]:2 =#
x = 2
#= REPL[2]:3 =#
y = 3
#= REPL[2]:4 =#
x + y
endResults can be stored into some variables, which we can inspect further.
julia> typeof(code_parse)
Expr
julia> dump(code_parse)
Expr
head: Symbol =
args: Array{Any}((2,))
1: Symbol x
2: Int64 2julia> typeof(code_parse_block)
Expr
julia> dump(code_parse_block)
Expr
head: Symbol block
args: Array{Any}((6,))
1: LineNumberNode
line: Int64 2
file: Symbol none
2: Expr
head: Symbol =
args: Array{Any}((2,))
1: Symbol x
2: Int64 2
3: LineNumberNode
line: Int64 3
file: Symbol none
4: Expr
head: Symbol =
args: Array{Any}((2,))
1: Symbol y
2: Int64 3
5: LineNumberNode
line: Int64 4
file: Symbol none
6: Expr
head: Symbol call
args: Array{Any}((3,))
1: Symbol +
2: Symbol x
3: Symbol yThe type of both multiline and single line expression is Expr with fields head and args. Notice that Expr type is recursive in the args, which can store other expressions resulting in a tree structure - abstract syntax tree (AST) - that can be visualized for example with the combination of GraphRecipes and Plots packages.
plot(code_expr_block, fontsize=12, shorten=0.01, axis_buffer=0.15, nodeshape=:rect)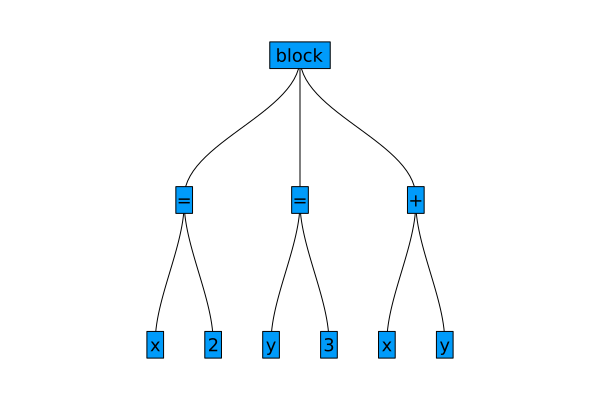
This recursive structure has some major performance drawbacks, because the args field is of type Any and therefore modifications of this expression level AST won't be type stable. Building blocks of expressions are Symbols and literal values (numbers).
A possible nuisance of working with multiline expressions is the presence of LineNumber nodes, which can be removed with Base.remove_linenums! function.
julia> Base.remove_linenums!(code_parse_block)
quote
x = 2
y = 3
x + y
endParsed expressions can be evaluate using eval function.
julia> eval(code_parse) # evaluation of :(x = 2)
2
julia> x # should be defined
2Exercise
Before doing anything more fancy let's start with some simple manipulation of ASTs.
Define a variable
codeto be as the result of parsing the string"j = i^2".Copy code into a variable
code2. Modify this to replace the power2with a power3. Make sure that the original code variable is not also modified.Copy
code2to a variablecode3. Replaceiwithi + 1incode3.Define a variable
iwith the value4. Evaluate the different code expressions using theevalfunction and check the value of the variablej.
Details
julia> code = Meta.parse("j = i^2")
:(j = i ^ 2)
julia> code2 = copy(code)
:(j = i ^ 2)
julia> code2.args[2].args[3] = 3
3
julia> code3 = copy(code2)
:(j = i ^ 3)
julia> code3.args[2].args[2] = :(i + 1)
:(i + 1)
julia> i = 4
4
julia> eval(code), eval(code2), eval(code3)
(16, 64, 125)Following up on the more general substitution of variables in an expression from the lecture, let's see how the situation becomes more complicated, when we are dealing with strings instead of a parsed AST.
Exercise
replace_i(s::Symbol) = s == :i ? :k : s
replace_i(e::Expr) = Expr(e.head, map(replace_i, e.args)...)
replace_i(u) = uGiven a function replace_i, which replaces variables i for k in an expression like the following
julia> ex = :(i + i*i + y*i - sin(z))
:((i + i * i + y * i) - sin(z))
julia> @test replace_i(ex) == :(k + k*k + y*k - sin(z))
[32m[1mTest Passed[22m[39mwrite a different function sreplace_i(s), which does the same thing but instead of a parsed expression (AST) it manipulates a string, such as
julia> s = string(ex)
"(i + i * i + y * i) - sin(z)"HINTS:
Use
Meta.parsein combination withreplace_iONLY for checking of correctness.You can use the
replacefunction in combination with regular expressions.Think of some corner cases, that the method may not handle properly.
Details
The naive solution
julia> sreplace_i(s) = replace(s, 'i' => 'k')
sreplace_i (generic function with 1 method)julia> @test Meta.parse(sreplace_i(s)) == replace_i(Meta.parse(s))Test Failed at REPL[1]:1
Expression: Meta.parse(sreplace_i(s)) == replace_i(Meta.parse(s))
Evaluated: (k + k * k + y * k) - skn(z) == (k + k * k + y * k) - sin(z)
ERROR: There was an error during testingdoes not work in this simple case, because it will replace "i" inside the sin(z) expression. We can play with regular expressions to obtain something, that is more robust
julia> sreplace_i(s) = replace(s, r"([^\w]|\b)i(?=[^\w]|\z)" => s"\1k")sreplace_i (generic function with 1 method)julia> @test Meta.parse(sreplace_i(s)) == replace_i(Meta.parse(s))Test Passedhowever the code may now be harder to read. Thus it is preferable to use the parsed AST when manipulating Julia's code.
If the exercises so far did not feel very useful let's focus on one, that is similar to a part of the IntervalArithmetics.jl pkg.
Exercise
Write function wrap!(ex::Expr) which wraps literal values (numbers) with a call to f(). You can test it on the following example
f = x -> convert(Float64, x)
ex = :(x*x + 2*y*x + y*y) # original expression
rex = :(x*x + f(2)*y*x + y*y) # result expressionHINTS:
use recursion and multiple dispatch
dispatch on
::Numberto detect numbers in an expressionfor testing purposes, create a copy of
exbefore mutating
Details
julia> function wrap!(ex::Expr)
args = ex.args
for i in 1:length(args)
args[i] = wrap!(args[i])
end
return ex
end
wrap! (generic function with 1 method)
julia> wrap!(ex::Number) = Expr(:call, :f, ex)
wrap! (generic function with 2 methods)
julia> wrap!(ex) = ex
wrap! (generic function with 3 methods)
julia> ext, x, y = copy(ex), 2, 3
(:(x * x + 2 * y * x + y * y), 2, 3)
julia> @test wrap!(ex) == :(x*x + f(2)*y*x + y*y)
[32m[1mTest Passed[22m[39m
julia> eval(ext)
25
julia> eval(ex)
25.0This kind of manipulation is at the core of some pkgs, such as aforementioned IntervalArithmetics.jl where every number is replaced with a narrow interval in order to find some bounds on the result of a computation.
Resources
Julia's manual on metaprogramming
David P. Sanders' workshop @ JuliaCon 2021
Steven Johnson's keynote talk @ JuliaCon 2019
Andy Ferris's workshop @ JuliaCon 2018
From Macros to DSL by John Myles White
Notes on JuliaCompilerPlugin
https://docs.julialang.org/en/v1/manual/faq/#What-does-the-...-operator-do? ↩︎
https://docs.julialang.org/en/v1/manual/functions/#Varargs-Functions ↩︎
Once you understand the recursive structure of expressions, the AST can be constructed manually like any other type. ↩︎